What is a Log Calculator?

A Log Calculator is a mathematical tool designed to help users perform logarithmic calculations quickly and accurately. Logarithms are fundamental to various fields of mathematics, engineering, and science. They provide a way to solve problems involving exponential growth or decay, simplify complex calculations, and understand mathematical relationships in a more manageable form.

Understanding Logarithms

To fully appreciate the utility of a Log Calculator, it’s essential to understand what a logarithm is. A logarithm is the inverse operation to exponentiation. In simpler terms, if you have an exponential equation of the form by=xb^y = xby=x, where $b$ is the base, $y$ is the exponent, and x is the result, the logarithm of x with base $b$ gives you $y$. This can be written as:

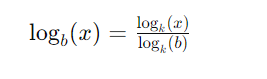
For instance, if you know that 102=10010^2 = 100102=100, then log⁡10(100)=2\log_{10}(100) = 2log10(100)=2.

Types of Logarithms

There are several types of logarithms, each used in different contexts:

1. Common Logarithms (Base 10):

   • Often referred to as base-10 logarithms, these are used in scientific calculations and are written as log⁡(x) or log⁡10(x). For example, log⁡10(100)=2.

2. Natural Logarithms (Base e):

   • These use the base e (approximately 2.718) and are denoted as ln⁡(x). They are commonly used in calculus and complex analysis. For instance, $=3$.

3. Binary Logarithms (Base 2):

   • These are used in computer science and information theory, denoted as log_2(x). For example, $3$.

Why Use a Log Calculator?

1. Complex Calculations Made Easy:

   • Logarithmic calculations can be complex, especially when dealing with large numbers or various bases. A Log Calculator simplifies these tasks by providing quick and accurate results, eliminating manual computation errors.

2. Educational Tool:

   • Students and educators use log calculators to understand and solve logarithmic problems, practice calculations, and explore mathematical concepts more effectively.

3. Scientific and Engineering Applications:

   • In fields like chemistry, physics, and engineering, logarithms are used to solve problems related to growth rates, pH levels, and signal processing. A Log Calculator helps in these areas by providing precise computations.

4. Data Analysis:

   • Logarithms are often used in data analysis to transform data for better visualization or interpretation. For example, converting data to a logarithmic scale can help in analyzing exponential growth trends.

5. Financial Calculations:

   • Logarithms are used in finance to calculate compound interest, investment growth, and other financial metrics. A Log Calculator can streamline these calculations, providing more accurate financial analysis.

How Does a Log Calculator Work?

A Log Calculator takes user inputs, such as the base of the logarithm and the number for which you want to find the logarithm. It then performs the calculation based on the logarithmic formula:

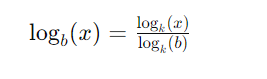
where k is a common base (often 10 or $e$) that the calculator uses for internal computations. The result is then displayed to the user.

Features of a Log Calculator

1. Multiple Bases:

   • Allows calculations with different bases, such as 10, $e$, and 2, as well as custom bases.

2. Precision:

   • Provides results with high precision, suitable for scientific and engineering applications.

3. Ease of Use:

   • User-friendly interface that allows users to input values easily and get results quickly.

4. Additional Functions:

   • Some calculators offer additional functions, such as calculating antilogarithms or performing logarithmic transformations.

5. Historical Data:

   • Stores previous calculations for reference, making it easier to track and compare results.